Complementi di Analisi Matematica

Anno Accademico 2003-2004

Laurea specialistica in Informatica

R.Stasi, V.M. Tortorelli

I prova in itinere, 31 marzo 2004

-------------------------------------------------------------

1.a- Dire se esiste il limite $(x,y)\to (0,0)$ di $f(x,y)=\frac {\tan (x^2+y^2)}{\sqrt{ x^4 +y^4}}$.

R.:

1.b- Si calcoli il differenziale della funzione $(x,y)\mapsto g(f(x,y))$ in $(1,1)$,

ove $f(x,y)= (xy, x^2-y^2)$, $g(u,v)= (\sin v, \cos u)$.

R.:

1.c- Si calcoli il polinomio di Taylor del terzo ordine in $(0,0,0)$ della funzione $(\sin xyz , \cos xyz )$.

R.:

2- Si calcolino i punti critici della funzione $f(x,y) = 2x^4-x^2 e^y +e^{4y}$ specificando se si tratta di punti di massimo o minimo relativo o meno.

R.:

3- Si calcoli $\frac{\partial z}{\partial x}_{\vert_{x=1,y=\sqrt{2}}}$ per la funzione definita implicitamente in un intorno di $(1,\sqrt{2}, 1)$ da

$f(x,y,z)=e^{x^2-y^2+z^2} -xz=0$.

R.:

4- Si calcoli il valore massimo e il valore minimo di $f(x,y,z)=2 {y} + 3{z}$,  sull'insieme $\left\{\begin{array}{ll}(x-1)^2 + (y-1)^2=1 &\\ (x-1)^2 + (z-1)^2=1&\ \end{array}\right.\$

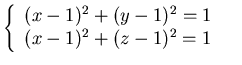
R.:

5- Si calcoli l'integrale di $f(x,y,z)=z$ sulla superficie definita da

$x^2 +y^2 +3z^2 = 4$ e $z>0$.

R.:

6- Per quali $\alpha$ il sottografico di $(x^2+y^2)^\alpha$ su $\vert x\vert +\vert y\vert \le 1$ ha volume finito?

R.: